[백준] 1790 - 수 이어 쓰기2

문제

문제 설명

Baekjoon Online Judge - 1790번 수 이어 쓰기2

1부터 N까지의 수를 이어서 쓰면 다음과 같이 새로운 하나의 수를 얻을 수 있다.

1234567891011121314151617181920212223…

이렇게 만들어진 새로운 수에서, 앞에서 k번째 자리 숫자가 어떤 숫자인지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N(1 ≤ N ≤ 100,000,000)과, k(1 ≤ k ≤ 1,000,000,000)가 주어진다. N과 k 사이에는 공백이 하나 이상 있다.

출력

첫째 줄에 앞에서 k번째 자리 숫자를 출력한다. 수의 길이가 k보다 작아서 k번째 자리 숫자가 없는 경우는 -1을 출력한다.

입출력 예

풀이

해설

1. 1부터 N까지 수를 이어적어 만든 수의 길이(숫자 개수)를 구한 뒤 k와 비교하여 예외처리

2. 앞에서부터 k번째 자리 숫자의 실제 수 구하기

   1. 앞에서부터 k번째 자리 숫자가 속한 수 구하기
   2. 2-i에서 구한 수의 몇번째 자리 숫자인지 구하기(최종 출력 값)

1-1. 자리수 별 숫자 개수 구하기

문제를 해결하기 위해서는 1부터 나열된 수들의 모임에서 특정 숫자가 몇 번째 자리에 위치한 숫자인지 그 관계를 알아야 한다.

따라서 숫자의 개수를 구해야 하는데, 각 수는 자신의 자리수만큼의 숫자로 구성되어 있으므로 각 자리수에 존재하는 수의 개수와 자리수를 곱하면 해당 자리수에 속한 수의 전체 길이를 구할 수 있다.

• 한 자리 수(1~9)는 9개가 존재하고 한 자리 수의 마지막 수인 9의 인덱스는 9
• 두 자리 수(10~99)는 180개가 존재하고 두 자리 수의 마지막 수인 99의 인덱스는 189
• 세 자리 수(100~999)는 2700개가 존재하고 세 자리 수의 마지막 수인 999의 인덱스는 2889
• 네 자리 수(1000~9999)는 36000개가 존재하고 네 자리 수의 마지막 수인 9999의 인덱스는 38889

1-2. k의 예외처리

위의 방법을 이용하여 1부터 N까지 수를 이어적었을 때 만들어지는 수의 길이를 구할 수 있다.

• N의 자리수보다 한 자리 작은 자리수의 마지막 수까지의 인덱스를 계산한다.

  -> 20은 두 자리수 이므로 한 자리수의 마지막 수인 9까지 인덱스를 구하면 9

• 이후에는 현재 자리수의 수들 중 N이 몇번째 수인지 구하고 다시 자리수를 곱한다.

  -> 두 자리 수들 중 20까지는 11개의 수가 존재하고, 각 수들은 모두 2자리 수이므로 11 * 2 = 22

• 위에서 구한 숫자 개수를 더하면 총 숫자 개수를 구할 수 있다!

  -> 9 + 22 = 31

따라서 수의 길이는 최대 31을 넘지 못하므로 입력된 k가 31 이상일 경우 -1을 반환한다.

2. k번째 자리 숫자 구하기

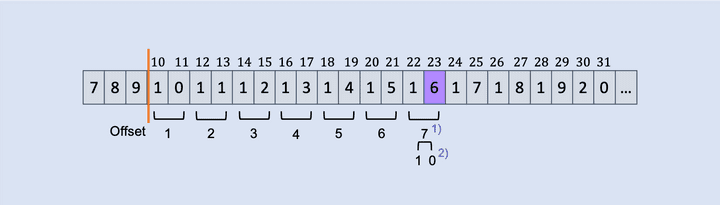
2-1. k번째 숫자가 속한 수

최종 목표인 k번째 숫자를 구하기에 앞서 k번째 숫자가 속한 수를 구하는 것이 더 쉽다.

k번째에서 k는 수가 아니라 위치 정보인 인덱스를 의미하므로 1)에서와 유사하게 자리수를 이용하면 된다.

단, 1)에서는 실제 수가 몇 번째인지 위치(인덱스)를 구했다면, 이번에는 반대로 위치(인덱스)를 통해 실제 수를 구해야 하므로, 자리수 별 마지막 수의 인덱스가 아닌 수 자체를 이용하고 자리수 나누기 연산을 해야한다.

• k의 자리수보다 한 자리 작은 자리수의 마지막 수를 구한다.

  -> 23은 두 자리수 이므로 한 자리수의 마지막 수인 9

• 이후에는 현재 자리수의 숫자들 중 k가 몇번째 숫자인지 구하고 자리수로 나눈다.

  -> k는 두 자리 수의 숫자들 중 (23 - 9)번째이고 각 수들은 모두 2자리 수
  14 / 2 = 7(두자리 수들 중 7번째 수)

• 위에서 구한 수를 더하면 k가 속한 수인 16을 도출할 수 있다.

2-2. k번째 숫자가 속한 수에서 최종 숫자 구하기

이제 거의 다왔다!!😂

k번째 숫자가 속한 수인 16에서의 위치는 2-1)에서 한 나누기 연산의 나머지를 보면 된다.

• 나머지가 0의 경우 : k번째 숫자가 속한 수의 자리수번째 수라는 의미로 수의 가장 마지막 숫자를 가리키는 것을 의미
• 나머지가 1 ~ (k번째 숫자가 속한 수의 자리수-1) 사이의 값일 경우 : k번째 숫자가 속한 수의 첫번째 숫자부터 1로 인덱싱하여 접근해야 함

아우 글로 쓰는게 더힘들다.

코드

import java.util.Scanner;

public class Baekjoon1790 {
	static Integer n, k;
	static String N;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt();
		k = sc.nextInt();
		N = Integer.toString(n);
		findNumberLocation();
	}
	
	static void findNumberLocation() {
		int nPlace = N.length();   // n의 자리수
		int nDigits = 0;           // n까지 이어붙인 수의 전체 길이(숫자 개수, 인덱스); k 예외처리를 위해 계산
        int underKPlace = 0;       // k번째 수의 자릿수 - 1
		int underKDigits = 0;      // (k번째 수의 자릿수 - 1)까지 숫자 개수

		// (N의 자리수 - 1)까지 숫자 개수 구하기(9개 + 180개 + 2700개 ...)
		for (int place=1; place<nPlace; place++) {
			nDigits += (9 * (int) Math.pow(10, place-1) * place);

            // k번째 수를 위해 (k번째 수의 자리수 - 1)까지의 숫자 개수, 자리수 기억
			if (k >= nDigits) {
				underKDigits = nDigits;
				underKPlace = place;
			}
		}

		// N의 자리수에 해당하는 수들의 숫자 개수를 구해 최종 nDigits 계산
		nDigits += (n - (int)(Math.pow(10, nPlace-1) - 1)) * nPlace;

		// k가 1부터 n까지 이어붙인 수의 전체 길이를 초과하는지 체크
		if (k > nDigits) {
			System.out.println(-1);
		} else {
			// k번째 수의 자리수에 해당하는 수들의 개수를 구해 최종 k번째 숫자 구하기
			int q = (k - underKDigits) / (underKPlace + 1);   // 몫
            int r = (k - underKDigits) % (underKPlace + 1);   // 나머지
			Integer target = ((int) Math.pow(10, underKPlace) - 1) + q;
			if (r == 0) {
				System.out.println(Integer.toString(target).charAt(underKPlace));   // 수의 마지막 인덱스 접근
			} else {
				System.out.println(Integer.toString(++target).charAt(--r));   // 나머지가 존재할 경우 target 다음 수에서 인덱싱하여 접근
			}
		}
	}
}

💡

• 수학 문제들은 풀다보면 뭔가 겸손해지는 느낌…ㅎㅎ
• 자리수 별 숫자 개수를 구하는 규칙만 찾으면 그 다음은 구현 문제~~
• 풀이를 자세하게 정리하니까 시간은 오래걸리지만 확실히 머리에서 정리가 된다.