희소 배열(Sparse Table)
배열 원소의 개수가 무조건 배열의 length 값보다 작은 배열
데이터가 저장되지 않은 경우가 더 많은 희소 행렬과 같이, 희소 배열은 배열의 원소 위치가 연속적이지 않은 배열을 말함
이러한 희소배열의 특징을 이용해 그래프의 사이클을 탐색해나가는 문제를 풀 수 있다.
희소 배열 알고리즘
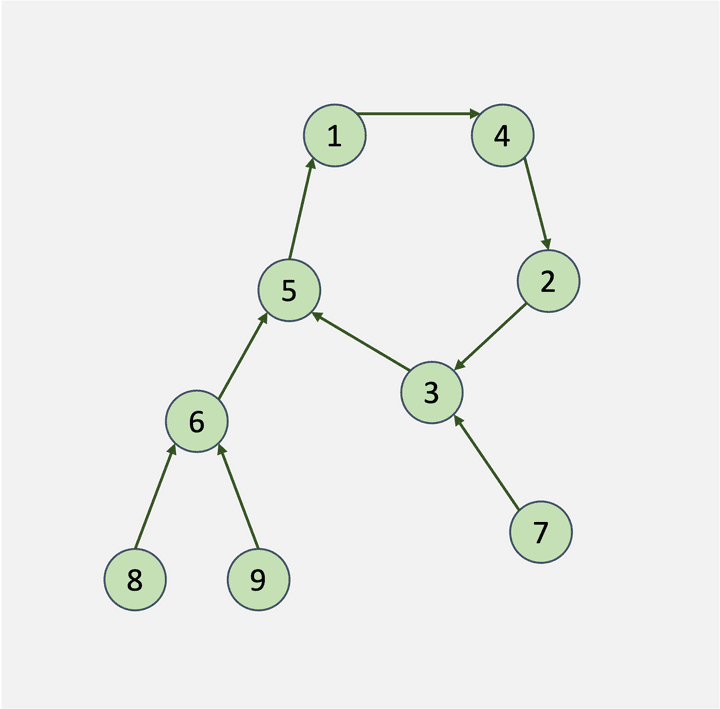
다음과 같이 사이클이 있는 그래프가 존재하고, 특정 정점(v)에서 시작해 n개의 간선을 이동해 도착할 수 있는 정점을 구한다고 생각해보자.
일반적으로는 간선 1개를 n번씩 이동하여 도착하는 정점을 찾는 방법을 떠올릴 것이다.
하지만 위의 문제를 반복적으로 풀어야 한다면? 모든 v정점에 대해 n개의 간선만큼씩 이동한다면 수없이 많이 이동해야 한다. 게다가 위 그래프는 사이클이 존재하기때문에, 어느 순간부터는 같은 이동을 반복하게될 것이다.
이 문제를 희소 배열로 해결해보자.
만약 1번 정점에서 시작해 7개의 간선을 이동해 도착할 수 있는 정점을 구한다면 이동 횟수는 다음과 같을 것이다.
7 = 4 + 2 + 1
7개의 간선을 이동한다고 해서 1번 이동하는 간선을 7개 거쳐가는 것이 아니다.
1번에서 4번 이동하여 5번에 도착, 5번에서 2번 이동하여 4번에 도착, 마지막으로 4번에서 1번 이동하여 2번으로 도착한다면 이동 횟수는 7번에서 3번으로 줄어들게 된다.
이처럼 간선을 1개씩 이동하지 말고, 1개, 2개, 4개, 8개, … 와같이 1부터 log n개까지 한번에 이동하고, 이렇게 도달한 정점을 배열에 저장한다면 몇 개의 간선도 빠르게 이동할 수 있다.
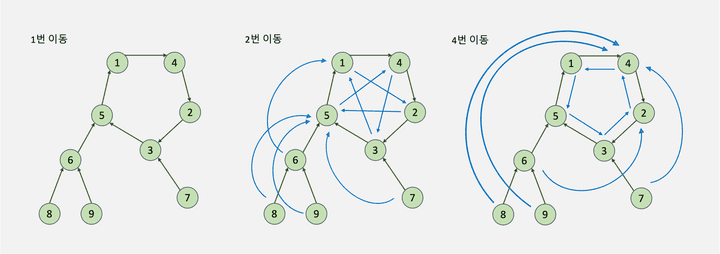
| 이동 횟수 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1번 이동 | 4 | 3 | 5 | 2 | 1 | 5 | 3 | 6 | 6 |
| 2번 이동 | 2 | 5 | 1 | 3 | 4 | 1 | 5 | 5 | 5 |
| 4번 이동 | 5 | 4 | 2 | 1 | 3 | 2 | 4 | 4 | 4 |
위 테이블은 사이클이 존재하는 그래프의 이동 노드를 표현한 것이므로, 각 행의 원소 개수가 열의 개수보다 작은 희소 배열로 표현되는 것을 알 수 있다.
이런 특성을 이용해 1 ~ log n 까지 이동하여 도착하는 정점을 희소 배열에 저장해둠으로써 사이클이 존재하는 그래프에서의 간선 이동을 빠르고 쉽게 해결할 수 있다.
희소 배열 알고리즘 구현
// 희소 배열
static int[][] sparseTable = new int[logn+1][n+1]; // 1차원 배열 길이는 이동 횟수를, 2차원 배열 길이는 총 정점의 길이를 의미
// 희소 배열 생성하여 각 정점의 이동 횟수별 도착 정점 기록
public static void makeSparseTable() {
// 1번 이동해서 도착하는 정점
for (int i=1; i<=n; i++) {
sparseTable[0][i] = arr[i];
}
// log n번까지 이동해서 도착하는 정점
for (int k=1; k<logn+1; k++) {
for (int i=1; i<=n; i++) {
int next = sparseTable[k-1][i];
sparseTable[k][i] = sparseTable[k-1][next];
}
}
}
// v 정점에서 출발하여 n개의 간선을 이동하여 도착한 정점 찾기
public static int query(int n, int v) {
for (bit=size-1; bit>=0; bit--) {
if ((n & (1<<bit)) != 0) {
v = sparseTable[bit][v];
}
}
}